Vector Spaces
교재 : Linear System Theory and Design $4_{th}$ Ed. by Chen, Oxford, 2013
Vector space
스칼라 필드 $ \textit{K} (실수 or 복소수)$에 대한 Vector space $ \textit{V}$
Definition : $\textit{V}$ 는 공집합이 아니며
1. Vector Addition : for any $\textit{u, v} \in V$, a sum $\textit{u+v} \in V$
2. Scalar Multiplication : any $\textit{u} \in V$, $\textit{k} \in K$, a product $\textit{ku} \in V$
$\textit{u, v, w} \in V$ : vector space에 있는 element를 vector 라고 부른다.
8가지 공리를 만족
1. $(u+v) + w = u + (v+w) $ : 결합 법칙, associativity
2. for any $\textit{u} \in V$, zero vector, 영벡터
$$ u+0 = 0+u = u $$
3. for each $\textit{u} \in V$, $negative$ of $u$, $-u$
$$ u+(-u)=(-u)+u=0$$
4. $ u+v=v+u$
5. for any scalar $\textit{k} \in K$, $k(u+v)=ku+kv$, 분배 법칙
6. for any scalars $\textit{a, b} \in K$, $(a+b)u=au+bu$
7. for any scalars $\textit{a, b} \in K$, $(ab)u=a(bu)$
8. for the unit scalar $\textit{1} \in K$, $1u=u$
Vector space의 예시
1. 유클리드 공간 Euclidean space
definition : 유클리드 공간은 $\mathbb{R}^n$ 으로 정의되는 특정한 vector space로, 다음과 같은 추가적인 구조가 정의된 공간
- 내적 : 두 벡터간 내적 $u\cdot v$가 정의됨.
이를 통해 벡터의 크기$($길이$)$와 각도를 계산할 수 있음
- 거리와 크기 : 벡터의 크기 norm은 $ \left\| v\right\| = \sqrt{v\cdot v} $
두 벡터 사이의 거리, 유클리디안 거리 $ d(u,v)=\left\| u-v\right\| $
- 예시 : $\mathbb{R}^2$ : 2차원 평면 공간, x-y좌표
$\mathbb{R}^3$ : 3차원 평면 공간. x-y-z 좌표
space $K^n$, 즉 K가 실수라면 $R^n$은 유클리디안 공간이고 이는 vector space 이다.
vector addition과 scalar multiplication을 각각의 space에 대해 정의해야 한다.
vector addition : $(a_1,a_2, \cdots , a_n)+(b_1,b_2, \cdots. b_n) = (a_1+b_1. a_2+b_2, \cdots, a_n+b_n)$
scalar multiplication : $k(a_1,a_2, \cdots , a_n) = (ka_1, ka_2, \cdots, ka_n)$
2. Polynomial space $P_n(t)$
스칼라 필드 K에 대한 모든 다항식 $p(t)$의 집합 $P_n(t)$ 는 차수가 n이하인 모든 다항식
$ P(t) = a_0 + a_1t + a_2t^2+ \cdots + a_st^s $
vector addition, scalar multiplication은 다항식에 대해 성립
3. Matrix space $M_{m,n}$
스칼라 필드 K에 대한 모든 $m x n$ matrix들의 집합
vector addition, scalar multiplication 성립
4. Function space $F(X)$
다항식을 비롯한 모든 함수가 포함됨
vector addition, scalar multiplication 성립
Linear Dependence and Independence 선형 의존, 선형 독립
definition : 만약 scalar $a_1, a_2, \cdots , a_m$ 이 K에서 존재하고,
$ a_1v_1 + a_2v_2 + \cdots + a_mv_m = 0 $ only when $a_1 = a_2 = \cdots = 0$이라면
vectors $ v_1, v_2. \cdots ,v_m$ in V 는 linearly independenet 하다.
그게 아니면, linearly dependent 하다.

Linear Combination 선형 조합
V는 스칼라장 K에 대한 vector space 이고, vector v in V is a linear combination of vectors $u_1, u_2, \cdots, u_m$ in V if there exist scalars $a_1, a_2, \cdots, a_m$ in K such that
$$ v = a_1u_1 + a_2u_2 + \cdots + a_mu_m $$
Spanning Sets 생성 집합
모든 가능한 linear combination
given $u1, u2, span\left\{u_1,u_2 \right\} = \left\{ au_1+bu_2 | a,b \in K \right\} $

Subspaces 부분 공간
subspace = subset of vector spaces, 또한 그것 자체도 vector space
모든 subspace는 원점을 지나야 한다!
예) vector space $V=R^2$

subset A : scalar multiplication 이 안됨, 영벡터가 포함 안됨
A는 V의 subspace가 아니고, vector space가 아니다.
subset C : 직선
vector addition, scalar multiplication 이 가능해 vector space이고, $V=R^2$의 subspace 이다.
V의 subspace들의 합집합은 V의 subspace가 아니고, 교집합은 subspace가 맞다.
행렬 A에 대한 row space : 행렬 A의 row의 linear combination으로 만들 수 있는 모든 집합. span{rows}
Let $ A = \begin{bmatrix} 2 & -1 & 0 \\ 2 & 1 & 0 \\ 0 & 1 & 1 \\ \end{bmatrix} $
우선 A를 echelon form으로 변환해야 한다.
L2 = L2 - L1
A = $\begin{bmatrix} 2 & -1 & 0 \\ 0 & 2 & 0 \\ 0 & 1 & 1 \\ \end{bmatrix} $
L3 = 2*L3-L2
A = $ \begin{bmatrix} 2 & -1 & 0 \\ 0 & 2 & 0 \\ 0 & 0 & 2 \\ \end{bmatrix} $
row space of A = span{ $\begin{pmatrix} 2 \\ -1 \\ 0 \end{pmatrix}, \begin{pmatrix} 0 \\ 2 \\ 0 \end{pmatrix}, \begin{pmatrix} 0 \\ 0 \\ 2 \end{pmatrix}$ }
만약 행렬 A의 row vector 들이 서로 linearly independent이면 row space의 basis가 된다.
행렬의 Row Space를 구성할 때, 각 행(row vector)이 꼭 선형 독립일 필요는 없습니다. 하지만, Row Space의 **기저(basis)**를 구성하는 벡터들은 반드시 선형 독립이어야 합니다.
행렬 A에 대한 column space
$ A^T = \begin{bmatrix} 2 & 2 & 0 \\ -1 & 1 & 1 \\ 0 & 0 & 1 \\ \end{bmatrix} $
L2 = L1 + 2*L2
$ A^T = \begin{bmatrix} 2 & 2 & 0 \\ 0 & 4 & 2 \\ 0 & 0 & 1 \\ \end{bmatrix} $
column space of A = span{ $\begin{pmatrix} 2 \\ 2 \\ 0 \end{pmatrix}, \begin{pmatrix} 0 \\ 4 \\ 2 \end{pmatrix}, \begin{pmatrix} 0 \\ 0 \\ 1 \end{pmatrix}$ }
A의 row vector를 span한 row space는, A를 전치한 $A^T$의 column vector를 span한 column space와 같다.
Ax=b 는 모든 b 에 대해 해를 가지고 있을까?

예를 들어 b = [0 0 0 0$]^T $ 일 때 x = [0 0 0$]^T$ 가 된다.
또한 b=[1 2 3 4$]^T$ 일 때 x=[1 0 0$]^T$이 된다. 이때 b는 A의 첫 번째 열과 같다.
우리는 선형 방정식 Ax=b에 대해 b벡터가 A의 column space에 존재할 때만 해를 구할 수 있다.
즉, b벡터가 A의 column의 linear combination으로 표현이 가능할 때 Ax=b에 대한 해를 구할 수 있다.
Gauss Elimination 가우스 소거법
gauss elimination, 즉 row reduction이란, 연립일차방정식을 풀이하는 알고리즘이다. 풀이 과정에서, 일부 미지수가 차츰 소거되어 결국 남은 미지수에 대한 linear combination으로 표현되면서 풀이가 완성된다.
row operations
1. 두 행을 바꾼다
2, 한 행에 0이 아닌 스칼라를 곱한다
3. 한 행에 스칼라를 곱하고 다른 행으로 더한다.
echelon : 계급, 계층, 지위
in echelon : 사다리꼴을 이루어

row echelon form 행사다리꼴 행렬 은 gauss elimination의 결과로 얻어지는 행렬이다.
조건 1. 0으로만 이루어진 행이 존재할 경우에 그 행은 행렬의 마지막 행이다.
2. 모든 0이 아닌 행의 pivot , 즉 leading coefficient 선행계수는 항상 그 위 행의 선행계수의 오른쪽에 있다.
* 만약 이때 모든 pivot이 1이면 reduced row echelon form 이다.
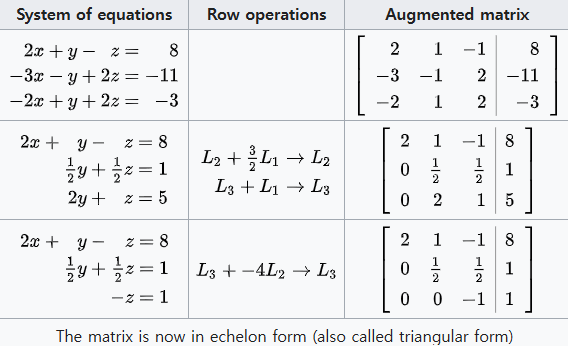
row reduction 절차 : 1행 밑에서 x를 제거한다, 그 후 2행 밑에서 y를 제거한다.
시스템을 triangular form으로 만든 이후 back substitution을 통해 각각의 미지수를 푼다.
Basis and Dimension
basis 기저
definition : A set $ S = {u_1, u_2, \cdots, u_n} $ of vectors is a basis of V if it has the following two properties :
1. S is linearly independent, 최소한의 개수
2. S spans V
dimension 차원 : 벡터 공간에서 차원은 선형 독립 벡터들로 이루어진 basis의 개수 로 정의된다.
즉, 차원은 벡터 공간을 생성 span 하는 데 필요한 최소한의 벡터 수 이다.
단일 벡터 자체에는 차원이 정의되지 않는다.
하지만 단일 벡터 $v \neq 0$로 생성된 벡터 공간의 차원은 1이다.
단일 벡터가 영벡터라면, 생성된 벡터 공간의 차원은 0이다.
vector space $ M_{2,3} $ 의 경우 basis :
$ \begin{bmatrix} 1& 0 & 0 \\0 & 0 & 0 \\ \end{bmatrix}, \begin{bmatrix} 0 & 1 & 0 \\0 & 0 & 0 \\ \end{bmatrix}, \begin{bmatrix} 0 & 0 & 1 \\0 & 0 & 0 \\ \end{bmatrix}, \begin{bmatrix} 0 & 0 & 0 \\1 & 0 & 0 \\ \end{bmatrix}, \begin{bmatrix} 0 & 0 & 0 \\0 & 1 & 0 \\ \end{bmatrix}, \begin{bmatrix} 0 & 0 & 0 \\0 & 0 & 1 \\ \end{bmatrix} $
차원 $dim M_{2,3} = 2 \times 3 = 6 $
vector space $ P_n(t)$ of all polynomials of degree $\leq n$ 의 경우
n+1차 polynomial의 set S = {$1, t, t^2, t^3 , \cdots, t^n$} 가 basis
차원 $ dim P_n(t) = n+1 $
Rank of matrics
definition : The $rank$ of a matrix A, written rank(A), is equal to the maximum number of linearly independent rows/columns of A
$$rank(A) = rank(A^T) $$
$ A = \begin{bmatrix} 1&2 \\ 2&3 \\ 3&0 \end{bmatrix} $
$ -6(\frac{3}{2}L_1 - L_2) = L_3 $, L1과 L2는 linearly independent
$ rank(A) = 2 $
$ B = \begin{bmatrix} 1&10 \\ 2&20 \\ 3&30 \end{bmatrix} $
$ rank(B) = 1 $, 최소 rank는 1이다.
matrix를 row reduction form으로 만들면 pivot column의 개수가 그 matrix의 rank 이다.
$ A = \begin{bmatrix} 1&2 \\ 2&3 \\ 3&0 \end{bmatrix} $
L2 = L2-2*L1 하면
$ RREF(A) = \begin{bmatrix} 1&2 \\ 0&-1 \\ 3&0 \end{bmatrix} $
L3=L3-3*L1하면
$ RREF(A) = \begin{bmatrix} 1&2 \\ 0&-1 \\ 0&-6 \end{bmatrix} $
L3=L3-6*L2하면
$ RREF(A) = >\begin{bmatrix} 1&2 \\ 0&-1 \\ 0&0 \end{bmatrix} $
RREP(A)에 2개의 pivot column이 있으므로 A의 rank는 2이다.
A "pivot column" in a matrix is
a column that contains a "pivot element", which is the leading non-zero entry in a row when the matrix is in row echelon form
Sums and direct sums
sum
U+W = {v : v = u+w, where $u \in U$ and $w \in W$ }
U와 W는 V의 subspace이면, U+W 도 V의 subspace이다.
$dim(U+W) = dim U + dim W - dim(U \cap W) $
$ U={1, 2}, W={3, 4} $ 이면 $ U +W = {1+2, 1+3, 2+3, 2+4}, U \cup W = {1, 2, 3, 4} $
direct sum
vector space V는 V의 subspace U와 W의 direct sum 이다. $ V = U \oplus W $ 오직 다음 두 조건을 만족할 때 :
1. $ V=U+W$
2. $ U \cap W = {0} $
영벡터는 모든 vector space의 필수적 구성 요소로, 공간의 독립성을 깨지 않는다.
Coordinates 좌표
V가 basis $ S={u_1,u_2,\cdots,u_n} $인 n-dimensional vector space라 하자.
그러면 any vector $ v \in V$는 basis vector S의 linear combination으로써 유일하게 표현될 수 있다.
$$ v = a_1u_1 + a_2u_2 + \cdots + a_nu_n $$
이런 n개의 scalar $a_1,a_2,\cdots,a_n$을 vector v의 basis S에 상대적인 coordinates 라고 한다. 주로 열벡터로 표현된다.
