2025. 1. 5. 23:11ㆍ선형시스템이론
Mappings, Functions
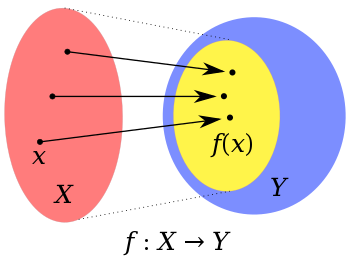
함수 function, 또는 사상 mapping : 어떤 집합의 각 원소를 다른 어떤 집합의 유일한 원소에 대응시키는 이항 관계이다.
정의역 domain : 함수가 어떤 값을 대응시키는지가 정의된 원소들로 구성된 집합
공역 codomain, targer set : 이 함수의 값들이 속하는 집합
치역 range : 함수의 모든 출력값의 집합. 즉, 정의역의 상 image 이다.
상 image : 어떤 함수에 대한 정의역의 원소에 대응하는 공역의 원소
원상 preimage : 어떤 함수에 대한 공역의 원소에 대응하는 정의역의 원소
그래프 graph : $(a, f(a)) : a \in A $
Composition of Mappings
$ f : A \to B, g : B \to C $ 일때, f와 g의 합성 $ g \circ f : A \to C $는 다음과 같다
$$ (g \circ f)(a) \equiv g(f(a)) $$
One-to-One and Onto Mappings
단사함수 injection function, 일대일 함수 one-to-one function : 정의역의 서로 다른 원소를 공역의 서로 다른 원소로 대응시키는 함수. 공역의 각 원소는 정의역의 원소 중 최대 한 원소의 상이다.
전사함수 surjective function, 위로의 함수 onto : 공역과 치역이 같은 함수
전단사 함수 bijection function, 일대일 대응 one-to-one correspondence : 두 집합 사이를 중복 없 모두 일대일로 대응시키는 함수. 전사 함수이며 단사 함수이다. 이 경우에만 inverse 가 존재
Linear Mappings
definition : V와 U가 같은 field K에 대해 vector space 이다. 이 때 mapping $ F : V \to U $는 아래 두 개의 조건을 충족하면
linear mapping 혹은 linear transformation이라고 불린다.
1. for any vectors $ v, w \in V, F(v+w) = F(v) + F(w) $
2. for any scalar k and vector $ v \in V, F(kv) = kF(v) $
-> additivity and homogeneity = linearity
linear operator : $ F : V \to V $
Matrices as Linear Mappings
mapping $ F : R^2 \to R^3 $
만약 $R^2$의 basis를 $(1,0), (0,1)$로 설정한다면 coordinates는 $(2,3)$
$(1,0), (1,1)$로 설정한다면 coordinates는 $(-1,3)$
만약 $R^3$의 basis를 $(1,0,0), (0,1,0), (0,0,1)$로 설정한다면 coordinates는 $(1,1,1)$
$$ mapping \begin{pmatrix}-1 \\ 3 \end{pmatrix} = \begin{pmatrix}1 \\ 1 \\ 1 \end{pmatrix} $$
linear mapping은 matrix는 아니지만, 만약 우리가 basis를 정하고 그걸로 coordinates를 나타내면,matrix로 표현될 수 있다.
Ax = y 라고 하면 A : $ X \to Y $ 이다. 행렬 A를 이용하여 mapping을 나타낼 수 있다.
여기서 x,y 는 coordinate이다
Kernel and Image of a Linear Mapping

$ F : V \to U $ 를 linear mapping 이라고 하자. 이 때 V는 domain, U는 codomain 이다.
kernel of F, $Ker(F)$, null space, $Null(F) = {v \in V : F(v) = 0} $
image of F, $ Im(F)$, range, $R(F)$ = {$u \in U$ : there exists $ v \in V$ for which $F(v) = u$}
일반적으로 위처럼 4개의 subspace로 나뉘지만, 어떤 경우에는 null space가 존재하지 않기도 한다.
$ F : V \to U $, $V:n \times 1,U:m \times 1, F:m \times n$ ,$ FV = U $
$ F^T : U \to V $, $F^T : n \times m$
inverse는 $u_1$에서 아예 $v_1$으로 가야 한다. inverse가 존재하려면 V와 U 모두에 null이 없어야 한다.
null : 영, 중요하지 않은
kernel : 핵심
null space : 선형 방정식 Ax=b에서, b가 0벡터 일 때 식을 만족시키는 모든 가능한 해 x에 대한 집합이다.
즉, 선형방정식 Ax=0의 해가 이루는 공간을 의미한다.
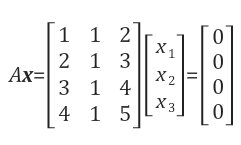
이때 해는 0벡터 x=[0 0 0$]^T$이다. 어떤 null space 이든지 반드시 0벡터는 포함된다.
또한 col1과 col2를 더하고 col3에 -1을 곱해 더해 주면 그 결과가 0벡터가 될 것이다.
즉 임의의 상수c를 곱한 x=c[1 1 -1$]^T$가 모두 해가 된다.
3차원 공간$(R^3)$에서 null space는 원점$(0벡터)$와 x=[1 1 -1$]^T$를 지나는 직선으로 표현된다.
nullspace도 vector space의 하나의 subspace 이다.
Rank and Nullity of a Linear Mapping
Nullity 는 Nullspace의 차원, 즉 nullspace의 basis를 이루는 linearly independent 벡터의 개수이다.
$$ Nullity(A) = dim(Nullspace(A)) $$
Ax=0의 해를 구하자!
$$ \begin{bmatrix} 1 & 2 & 3 \\ 4 & 5 & 6 \\ \end{bmatrix} \begin{bmatrix} x_1 \\ x_2 \\ x_3 \\ \end{bmatrix} = \begin{bmatrix} 0\\ 0\\ \end{bmatrix} $$
이를 augmented matrix로 나타내면
$$ \begin{bmatrix} 1 & 2 & 3 & 0 \\ 4 & 5 & 6 & 0 \\ \end{bmatrix} $$
A의 L2 = L2-4*L1 하면
$$ \begin{bmatrix} 1 & 2 & 3 & 0 \\ 0 & -3 & -6 & 0 \\ \end{bmatrix} $$ 으로 row echelon form 이 되었다.
$$ x_1 + 2x_2 + 3x_3 = 0 \\ -3x_2-6x_3=0 $$
이후 $ x_2 = -2x_3, x_1 = x_3 $ 이므로
$$ \begin{bmatrix} x_1 \\ x_2 \\ x_3 \\ \end{bmatrix} = x_3 \begin{bmatrix} 1 \\ -2 \\ 1 \\ \end{bmatrix}$$
그러니까 $$Nullspace(A) = span{ \begin{bmatrix} 1 \\ -2 \\ 1 \\ \end{bmatrix} } $$
이 때 Nullspace의 basis = $\begin{bmatrix} 1 \\ -2 \\ 1 \\ \end{bmatrix}$ 이다.
Nullity는 nullspace의 basis를 이루는 linearly independent 벡터의 개수이므로, $Nullity(A) = 1 $ 이다.
rank-nullity connection
n : A의 열의 개수
$Rank(A)+Nullity(A)=n$
$rank(A) = dim(range(A)) = dim(image(A))$
예제1.
행렬 A :
$$ A = \begin{bmatrix} 1 & 2 & 3 \\ 4 & 5 & 6 \\ \end{bmatrix} $$
설정 :
- A : 2 x 3 행렬 $(m = 2, n = 3)$
- b : 2 x 1 벡터$(항상 \mathbb{R}^2에 속함)$
Rank 계산 :
- $Rank(A) = 2$, 따라서 $Range(A)$는 $\mathbb{R}^2$의 2차원 전체 공간입니다.
결과 :
- b가 $\mathbb{R}^2$에 속하므로, $Ax=b$는 항상 해를 가집니다.
예제2.
행렬 A :
$$ A = \begin{bmatrix} 1 & 2 \\ 2 & 4 \\ 3 & 6 \\ \end{bmatrix} $$
설정 :
- A : 3 x 2 행렬 $(m = 3, n = 2)$
- b : 3 x 1 벡터$(항상 \mathbb{R}^3에 속함)$
Rank 계산 :
- $Rank(A) = 1$, 열벡터는 선형 종속
결과 :
- $Range(A)$는 $\mathbb{R}^3$의 1차원 부분 공간입니다.
- b가 $Range(A)$에 속하지 않으면, $Ax=b$는 해를 가지지 않습니다.
- 즉. b는 $\mathbb{R}^3$에 속하지만, A의 경우 특정 조건을 만족해야만 해가 존재합니다.
결론 :
- b의 차원은 항상 A의 행 개수 m과 동일하다.
- 하지만, b가 실제로 해를 가지려면, b가 $Range(A)$에 속해야 한다.
- $Range(A)$의 차원은 $Rank(A)$, 즉 A의 column space의 차원과 같다.
$ dim(b)=dim(Range(A))+dim(Null(A^T)) $
Ax=b
x : domain, b : codomain
$ A = \begin{bmatrix} 1 & 2 & 3 \\ 4 & 5 & 6 \\ \end{bmatrix} $
$A^T = \begin{bmatrix} 1 & 4 \\ 2 & 5 \\ 3 & 6 \\ \end{bmatrix} $
$dim(b)$ :
- $dim(b) = dim(\mathbb{R}^m) = m = 2$
$dim(Range(A))$ :
- $dim(Range(A)) = Rank(A) = 2$
$dim(Null(A^T))$ :
- $A^T y=0$를 만족하는 y들의 공간의 차원
- $A^T y= \begin{bmatrix} 1 & 4 \\ 2 & 5 \\ 3 & 6 \\ \end{bmatrix} \begin{bmatrix} y_1 \\ y_2\\ \end{bmatrix} = \begin{bmatrix} 0 \\ 0 \\ 0 \\ \end{bmatrix} $
- $ y_1 + 4y_2=0, \\ 2y_1+5y_2=0, \\ 3y_1+6y_2=0$
- 유일한 해는 $y = \begin{bmatrix} 0\\ 0\\ \end{bmatrix}$ 뿐이다.
- 영벡터로 생성된 벡터 공간의 차원은 0이다.
결론 : $ dim(b)=dim(Range(A))+dim(Null(A^T)) $ 은 $2=2+0$으로 성립한다.
'선형시스템이론' 카테고리의 다른 글
| phase plane vs phase portrait (0) | 2025.02.06 |
|---|---|
| Diagonalization : Eigenvalues and Eigenvectors (0) | 2025.01.31 |
| Inner Product Spaces, Orthogonality (0) | 2025.01.20 |
| Linear Mappings and Matrices (0) | 2025.01.07 |
| Vector Spaces (1) | 2025.01.02 |