2025. 1. 31. 14:45ㆍ선형시스템이론
Eigenvalue and Eigenvector
정의 : field $K$에 대한 vector space $V$ 위의 linear transformation $ A : V \to V $가 주어졌다고 하자.
만약 어떤 $ v \in V$와 $ \lambda \in K $가
- $ v \neq 0 $
- $Av = \lambda v$
를 만족시키면, $v$를 $A$의 고유벡터라고 하고, $\lambda$를 $A$의 $\left( v에 \; 대응하는 \right) $고윳값이라고 한다.
Eigen decomposition
다음 식 $$ AV = \lambda V$$
은 n차원의 열벡터인 고유벡터 V와 고윳값 $\lambda$로 구성되며,
각각의 고윳값이 다르다고 가정하면
$$ Av_1 = \lambda_1 v_1 \\ Av_2 = \lambda_2 v_2 \\ \vdots \\ Av_n = \lambda_n v_n $$
이는 $$ A \begin{bmatrix} v_1 & v_2 & \cdots & v_n \end{bmatrix} = \begin{bmatrix} v_1 & v_2 & \cdots & v_n \end{bmatrix} \begin{bmatrix} \lambda_1 & 0 & \cdots & 0 \\\ 0 & \lambda_2 & 0 & 0 \\ \vdots & \vdots & \ddots & \vdots \\ 0 & 0 & \cdots & \lambda_n \\ \end{bmatrix}$$
$ A=VDV^{-1}$ : eigen decomposition
이는 similar transform의 하나의 예시이며 형태가 같다.
A행렬을 diagonalize 하였다!
eigenvector는 eigen space에서의 basis vector이다.
$v_1$은 D가 존재하는 space에서의 basis vector와 같다.
Eigen decomposition : eigenvalue가 complex라면
만약 A가 symmetric 이라면 eigenvalue는 real이 보장된다.
A의 element는 다 real이고, eigenvalue가 complex라면 당연히 eigenvector도 complex이다.
- $\lambda = a \pm jb$
- $v = u \pm jv$
기존방법 :
$$ A = VDV^{-1} = \begin{bmatrix} u+jv & u-jv \end{bmatrix} \begin{bmatrix} a+jb & 0 \\ 0 & a-jb \end{bmatrix} {\begin{bmatrix} u+jv & u-jv \end{bmatrix}}^{-1} $$
새로운 방법 :
consider $ P = \begin{bmatrix} -0.5j & 0.5 \\ 0.5j & 0.5 \end{bmatrix} $, $P^{-1} = \begin{bmatrix} j & -j \\ 1 & 1 \end{bmatrix} $
$$ A = VDV^{-1} = VIDIV^{-1} = V \left( P P^{-1} \right) D \left( P P^{-1} \right) V^{-1} = VP \;\; P^{-1}DP \;\; { \left( VP \right) }^{-1} $$
$$ VP = \begin{bmatrix} v & u \end{bmatrix} $$
$$ P^{-1}DP = \begin{bmatrix} a & -b \\ b & a \end{bmatrix} $$
$$ \therefore \quad A = \begin{bmatrix} u+jv & u-jv \end{bmatrix} \begin{bmatrix} a+jb & 0 \\ 0 & a-jb \end{bmatrix} {\begin{bmatrix} u+jv & u-jv \end{bmatrix}}^{-1} = \begin{bmatrix} v & u \end{bmatrix} \begin{bmatrix} a & -b \\ b & a \end{bmatrix} { \begin{bmatrix} v & u \end{bmatrix} }^{-1} $$
$$ \left( \; if \quad P = \begin{bmatrix} -0.5j & 0.5 \\ 0.5j & 0.5 \end{bmatrix} \; \right) $$
autonomous linear system : $\dot{x} = Ax $
Autonomous : No input $\left( u=0 \right) $
풀어쓰면
$$ \begin{bmatrix} \dot{x_1} \\ \dot{x_2} \\ \vdots \\ \dot{x_n} \end{bmatrix} = \begin{bmatrix} 1 & 1 & 0 & \cdots & 1 \\ 2 & -1 & 7 & \cdots & -1 \\ \vdots & \vdots & \vdots & \ddots & \vdots \\ 1 & 0 & 0 & \cdots & 1 \end{bmatrix} \begin{bmatrix} x_1 \\ x_2 \\ \vdots \\ x_n \end{bmatrix} $$
이의 해는 $$ \dot{x_1} = x_1 + x_2 + \cdots + x_n \\ \dot{x_2} = 2x_1 - x_2 + 7x_3 + \cdots - x_n \\ \vdots $$ 복잡하게 coupled dynamics로 되어 있다.
하지만 system matrix $A= \begin{bmatrix} 1 & 0 & 0 & \cdots & 0 \\ 0 & 2 & 0 & \cdots & 0 \\ \vdots & \vdots & \vdots & \ddots & \vdots \\ 0 & 0 & 0 & \cdots & 5 \end{bmatrix} $처럼 대각화 되었다면,
그 해는 $$ \dot{x_1} = x_1 \\ \dot{x_2} = 2x_2 \\ \vdots \\ \dot{x_n} = 5x_n $$이며
$$ x_1 = x_{10}e^t \\ x_2=x_{20}e^{2t} \\ \vdots \\ x_n=x_{no}e^{5t} $$ 로 계산될 수 있다! uncoupled dynamics
nonautonomous linear system : $ \dot{x} = Ax + Bu \\ y = Cx + Du $ : state equation과 output equation
$\left ( 참고로 \quad 이것은 \dot{x} = f \left( x, u, t \right) 와 같다. gradient를 생각. \right ) $
전달함수에서 분모의 차수 n이 분자의 차수 m보다 크면 $ \left( strictly \quad proper \right) $ D는 거의 0이 된다
1. 만약 eigenvalue $\lambda $ 가 모두 다르면, eigenvector도 모두 다르다
2. 만약 $\lambda$가 반복된다면? eigenvector가 다를 수도 있지만, 다르지 않을 수 도 있다
nullspace vs eigenspace
nullspace는 어떤 행렬 $A$에 대해 $Ax=0$을 만족하는 모든 벡터 $x$들의 공간이다.
$$ Null \left ( A \right ) = \left\{ x \in \mathbb{R}^n \;|\; Ax = 0 \right\} $$
eigenspace는 특정한 고윳값 $\lambda$에 대한 고유벡터들로 이루어진 공간이다.
$$ Eig \left( A, \lambda \right) = \left\{ x \neq 0 \;|\; \left( A - \lambda I \right) x = 0 \right\} $$
- 즉, 행렬 $A$에 대해 $Ax=\lambda x$를 만족하는 모든 non-trivial 한 $x$벡터들의 집합
- 특정 $\lambda$에 대한 eigenspace는 nullspace의 개념과 비슷하지만, $A - \lambda I$의 nullspace를 구하는 것이다.
Algebraic Multiplicity 대수적 중복도
정의 : 행렬 A의 특성 방정식 $$ det \left( A-\lambda I \right) = 0 $$
에서 고윳값 $\lambda$가 몇 번 중복되는지
예제 1:
$$ A = \begin{bmatrix} 4 & 0 \\ 0 & 4 \end{bmatrix} $$
- 특성방정식 : $det \left( A-\lambda I \right) = {\left( 4 - \lambda \right)}^2 = 0 $
- 고윳값 $\lambda = 4$의 algebraic multiplicity는 2이다.
Geometric Multiplicity 기하적 중복도
정의 : 어떤 고윳값에 대응하는 eigenspace의 차원.
예제 1:
$$ A = \begin{bmatrix} 4 & 0 \\ 0 & 4 \end{bmatrix} $$
$$ A-4I = \begin{bmatrix} 4-4 & 0 \\ 0 & 4-4 \end{bmatrix} = \begin{bmatrix} 0 & 0 \\ 0 & 0 \end{bmatrix} $$
$\lambda$에 해당하는 eigenspace는
$$ \begin{bmatrix} 0 & 0 \\ 0 & 0 \end{bmatrix} \begin{bmatrix} x_1 \\ x_2 \end{bmatrix} = \begin{bmatrix} 0 \\ 0 \end{bmatrix} $$
모든 벡터 $ x = \begin{bmatrix} x_1 \\ x_2 \end{bmatrix} $ 가 null space에 속한다.
null space는 전체 $\mathbb{R}^2$이고, 따라서 null sapce의 차원은 2이다.
따라서 Geometric multiplicity가 2가 된다.
- 항상 Algebraic mulitiplicity가 Geometric multiplicity 보다 크거나 같다.
- 행렬이 대각화가 가능하려면 두 개가 동일해야 한다.
만약 다르면? 대각화 불가..
Jordan decomposition을 사용
$$ Av = \lambda v $$
$ \left( A - \lambda I \right) v_1 = 0 $ : $v_1$ 은 eigenvector
$ \left( A - \lambda I \right) v_2 = v_1 $ : $v_2$는 generalized eigenvector
$\to$ $ { \left( A - \lambda I \right) }^2 v_2 = 0 $
$\to$ $v_2$는$ { \left( A - \lambda I \right) }^2 $의 nullspace에 존재
$ Av_1 = \lambda v_1 $
$ Av_2 = v_1 + \lambda v_2 $
$ A \begin{bmatrix} v_1 & v_2 \end{bmatrix} = \begin{bmatrix} v_1 & v_2 \end{bmatrix} \begin{bmatrix} \lambda & 1 \\ 0 & \lambda \end{bmatrix} $
$ \therefore \; A = \begin{bmatrix} v_1 & v_2 \end{bmatrix} \begin{bmatrix} \lambda & 1 \\ 0 & \lambda \end{bmatrix} { \begin{bmatrix} v_1 & v_2 \end{bmatrix} }^{-1} $ : Jordan decomposition
$ \begin{bmatrix} \lambda & 1 \\ 0 & \lambda \end{bmatrix}$ : Jordan matrix
예시
$$ A = \begin{bmatrix} 5 & 1 \\ 0 & 5 \end{bmatrix} $$
이 행렬의 특성 방정식은
$$ det \left( A - \lambda I \right) = \begin{bmatrix} 5 - \lambda & 1 \\ 0 & 5 - \lambda \end{bmatrix} = {\left( 5 - \lambda \right)}^2 = 0 $$
고윳값 $ \lambda = 5 $ 에 대해
- Algebraic multiplicity = 2
$$ A-5*I = \begin{bmatrix} 0 & 1 \\ 0 & 0 \end{bmatrix} $$
$$ \begin{bmatrix} 0 & 1 \\ 0 & 0 \end{bmatrix} \begin{bmatrix} x_1 \\ x_2 \end{bmatrix} = \begin{bmatrix} 0 \\ 0 \end{bmatrix} $$
$ A-5*I $의 nullspace를 구하니 $x = \begin{bmatrix} x_1 \\ x_2 \end{bmatrix} = \begin{bmatrix} x_1 \\ 0 \end{bmatrix} $ 이므로,
eigenspace $Eig \left( A, \lambda = 5 \right) = span \left\{ \begin{bmatrix} 1 \\ 0 \end{bmatrix} \right\} $이다.
원점을 지나는 직선이므로 1차원이다.
- Geometric multiplicity = 1
Algebraic multiplicity와 Geometric multiplicity가 같지 않아 대각화가 불가능하며 Jordan decomposition을 수행해야 한다.
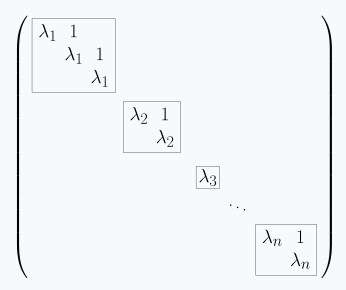
jordan block : jordan form에서 같은 eigenvalue들끼리 묶은 것. 주대각선에 고윳값이 있고, 바로 위에 1이 배치된 구조.
이를 위해 Generalized Eigenvector가 필요하다. Generalized Eigenvector는 다음을 만족하는 벡터 v이다.
$$ \left( A - 5I \right) v = u $$
여기서 u는 기존의 고유 벡터 $ \begin{bmatrix} 1 \\ 0 \end{bmatrix} $이다.
$$ \left( A - 5I \right) v = \begin{bmatrix} 1 \\ 0 \end{bmatrix} $$
$$ \begin{bmatrix} 0 & 1 \\ 0 & 0 \end{bmatrix} \begin{bmatrix} v_1 \\ v_2 \end{bmatrix} = \begin{bmatrix} 1 \\ 0 \end{bmatrix} $$
$$ v_2=1, \quad v = \begin{bmatrix} 0 \\ 1\end{bmatrix} $$
Jordan basis $P = \begin{bmatrix} eigenvector & generalied \; eigenvector \end{bmatrix} = \begin{bmatrix} u & v \end{bmatrix} = \begin{bmatrix} 1 & 0 \\ 0 & 1 \end{bmatrix} $
결론 : Jordan Form 구성
$$ J = \begin{bmatrix} 5 & 1 \\ 0 & 5 \end{bmatrix} $$
$$ A = P J P^{-1} $$
Matrix Exponential
taylor series 에서
$$ e^t = 1 + t + \frac{t^2}{2!} + \frac{t^3}{3!} + \cdots + \frac{t^k}{k!} + \cdots $$
행렬에 대해 정의한다면
$$ e^A \overset{\underset{\mathrm{def}}{}}{=} I + A + \frac{A^2}{2!} + \frac{A^3}{3!} + \cdots + \frac{A^k}{k!} + \cdots $$
$$ A = PBP^{-1} \\ PBP^{-1} PBP^{-1} = PB^2P^{-1} $$ 라 하면
$ \begin{align} \therefore \; e^A = e^{ PBP^{-1} } & = I + PBP^{-1} + \frac{ PB^2P^{-1}}{2!} + \frac{ PB^3P^{-1}}{3!} + \cdots \\ & = P \left( I + B + \frac{B^2}{2!} + \frac{B^3}{3!} + \cdots \right) P^{-1} \\ & = P e^B P^{-1} \end{align} $
참고로 $ e^D = e^{\begin{bmatrix} a & 0 \\ 0 & b \end{bmatrix} } = \begin{bmatrix} e^a & 0 \\ 0 & e^b \end{bmatrix} $
원래 $ e^{\begin{bmatrix} a & b \\ c & d \end{bmatrix} } \neq \begin{bmatrix} e^a & e^b \\ e^c & e^d \end{bmatrix} $
Let
$ \begin{align} A = VDV^{-1} & = \begin{bmatrix} u+jv & u-jv \end{bmatrix} \begin{bmatrix} a+jb & 0 \\ 0 & a-jb \end{bmatrix} {\begin{bmatrix} u+jv & u-jv \end{bmatrix}}^{-1} \\ & = \begin{bmatrix} v & u \end{bmatrix} \begin{bmatrix} a & -b \\ b & a \end{bmatrix} { \begin{bmatrix} v & u \end{bmatrix} }^{-1} \end{align} $
$ \begin{align} \therefore \; e^A = V e^D V^{-1} & = V e^{\begin{bmatrix} a+jb & 0 \\ 0 & a-jb \end{bmatrix} }V^{-1} \\ & = V \begin{bmatrix} e^{a+jb} & 0 \\ 0 & e^{a-jb} \end{bmatrix} V^{-1} \\ & = V e^a \begin{bmatrix} e^{jb} & 0 \\ 0 & e^{-jb} \end{bmatrix} V^{-1} \\ & = V e^a \begin{bmatrix} \cos b + j\sin b & 0 \\ 0 & \cos b - j\sin b \end{bmatrix} V^{-1} \\ & = e^a V PP^{-1} \begin{bmatrix} \cos b + j\sin b & 0 \\ 0 & \cos b - j\sin b \end{bmatrix} PP^{-1} V^{-1} \\ & = e^a \begin{bmatrix} v & u \end{bmatrix} \begin{bmatrix} \cos b & -\sin b \\ \sin b & \cos b \end{bmatrix} { \begin{bmatrix} v & u \end{bmatrix} }^{-1} \end{align} $
$$ e^{\begin{bmatrix} a & -b \\ b & a \end{bmatrix} } = e^a \begin{bmatrix} \cos b & -\sin b \\ \sin b & \cos b \end{bmatrix} $$
Let $ M = \begin{bmatrix} a & -b \\ b & a \end{bmatrix} = aI + bJ = a \begin{bmatrix} 1 & 0 \\ 0 & 1 \end{bmatrix} + b \begin{bmatrix} 0 & -1 \\ 1 & 0 \end{bmatrix} $
$ \left( I^2 = I, \quad J^2 = \begin{bmatrix} 0 & -1 \\ 1 & 0 \end{bmatrix} \begin{bmatrix} 0 & -1 \\ 1 & 0 \end{bmatrix} = -I \right) $
$$ e^M = e^{aI + bJ} = e^a e^{bJ} $$
$$ \begin{align}
e^{bJ} &= I + bJ + \frac{(bJ)^2}{2!} + \frac{(bJ)^3}{3!} + \frac{(bJ)^4}{4!} + \frac{(bJ)^5}{5!} + \cdots \\
&= I + bJ - \frac{b^2I}{2!} - \frac{b^3J}{3!} + \frac{b^4I}{4!} + \frac{b^5J}{5!} + \cdots \\
&= \left( I - \frac{b^2I}{2!} + \frac{b^4I}{4!} + \cdots \right) + \left( bJ - \frac{b^3J}{3!} + \frac{b^5J}{5!} + \cdots \right) \\
&= \cos b \, I + \sin b \, J \\
&= \cos b \begin{bmatrix} 1 & 0 \\ 0 & 1 \end{bmatrix} + \sin b \begin{bmatrix} 0 & -1 \\ 1 & 0 \end{bmatrix} \\
&= \begin{bmatrix} \cos b & -\sin b \\ \sin b & \cos b \end{bmatrix}
\end{align} $$
$ \therefore \; e^{\begin{bmatrix} a & -b \\ b & a \end{bmatrix} } = e^M = e^a \begin{bmatrix} \cos b & -\sin b \\ \sin b & \cos b \end{bmatrix} $
nilpotent matrix : 양의 정수 $k$에 대해, $N^k = 0$을 만족하는 square matrix $N$
예시1.
$A = \begin{bmatrix} 0 & 1 \\ 0 & 0 \end{bmatrix}$ 은 $A^2 = 0$ 이기 때문에 index 2 에서 nilpotent 하다.
예시2.
더 일반적으로, 주대각성분이 0인 n차원 triangular matrix는 index $ \leq n $에서 nilpotent 하다.
$ B = \begin{bmatrix} 0 & 2 & 1 & 6 \\ 0 & 0 & 1 & 2 \\ 0 & 0 & 0 & 3 \\ 0 & 0 & 0 & 0 \end{bmatrix}$ 는 index 4에서 nilpotent 하다. $B^4 = \begin{bmatrix} 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 \end{bmatrix} $
Cayley-Hamilton 정리
고윳값이 포함된 방정식인 특성방정식에 고윳값 대신 행렬을 넣어도 성립한다.
$$ A = \begin{bmatrix} a &b \\ c & d \end{bmatrix}$$
특성방정 : $$ det \left( A - \lambda I \right) = 0 $$
$$ \begin{vmatrix} a-\lambda & b \\ c & d-\lambda \end{vmatrix} = {\lambda}^2 - \left( a+d \right) \lambda + ad - bc = 0 $$
$\lambda$대신 A를 대입
$$ A^2 - \left( a+d \right) A + \left( ad - bc \right) I = 0 \\ A^2 = \left( a+d \right) A - \left( ad - bc \right) I $$
Reference
https://en.wikipedia.org/wiki/Jordan_normal_form
https://deep-learning-study.tistory.com/324
'선형시스템이론' 카테고리의 다른 글
| phase plane vs phase portrait (0) | 2025.02.06 |
|---|---|
| Inner Product Spaces, Orthogonality (0) | 2025.01.20 |
| Linear Mappings and Matrices (0) | 2025.01.07 |
| Linear Mappings (0) | 2025.01.05 |
| Vector Spaces (0) | 2025.01.02 |